Effect Size

Effect Size: What It Is and Why It Matters More Than Statistical Significance

A result can be statistically significant — yet practically meaningless. Learn how effect size reveals the real-world impact of research findings.

Introduction: The Hidden Problem with p-values

You’ve probably seen headlines like:

“New Study Shows Coffee Improves Memory!”

But what if the improvement was just 0.3 points on a 100-point test?

Technically “significant” — but is it meaningful?

This is where effect size comes in.

While p-values tell us whether an effect exists, effect size tells us how large that effect is — a crucial distinction often overlooked in science, education, and media.

In this article, you’ll learn:

What effect size really means
How to calculate and interpret common measures (like Cohen’s d)
Why it’s essential for sound scientific reasoning
Best practices for reporting it in research

Let’s go beyond significance testing and focus on what truly matters: practical importance.

What Is Effect Size?

Effect size is a quantitative measure of the magnitude of a phenomenon. Unlike p-values, which depend heavily on sample size, effect size provides a standardized metric that reflects the strength of a relationship or difference — independent of how many people were studied.

In simple terms:

p-value: “Is there an effect?” → answers statistical significance

Effect size: “How big is the effect?” → answers practical significance

For example:

Two teaching methods differ by 5 points in average test scores.

With a small class, the difference might not be significant (high p-value).

With a huge sample, even a 0.5-point difference could be “significant” (low p-value).

But only effect size tells you whether those 5 (or 0.5) points matter in practice.

Effect Size vs. Hypothesis Testing: Key Differences

Feature	p-value / Null Hypothesis Testing	Effect Size
Purpose	Test if an effect is likely due to chance	Measure the strength of the effect
Depends on sample size	Yes — larger samples increase significance	No — it’s independent of N
Tells you	Whether an effect exists	How large the effect is
Common misuse	Mistaking statistical significance for importance	Ignoring it altogether

Key insight: A small effect can be highly significant with a large sample — but still too weak to justify policy changes, clinical use, or educational reform.

Side-by-side comparison showing how large samples can detect tiny, irrelevant effects.

How to Calculate Effect Size: Cohen’s d

One of the most widely used measures is Cohen’s d, ideal for comparing the means of two groups.

Formula:

$d = \frac{\bar{X}_1 - \bar{X}_2}{s_{\text{pooled}}}$

Where:

$\bar{X}_1$ and $\bar{X}_2$ are the means of the two groups

$s_{\text{pooled}}$ is the pooled standard deviation:

$s_{\text{pooled}} = \sqrt{\frac{(n_1 - 1)s_1^2 + (n_2 - 1)s_2^2}{n_1 + n_2 - 2}}$

If group sizes are equal, you can approximate $s_{\text{pooled}}$ as the average of the two standard deviations

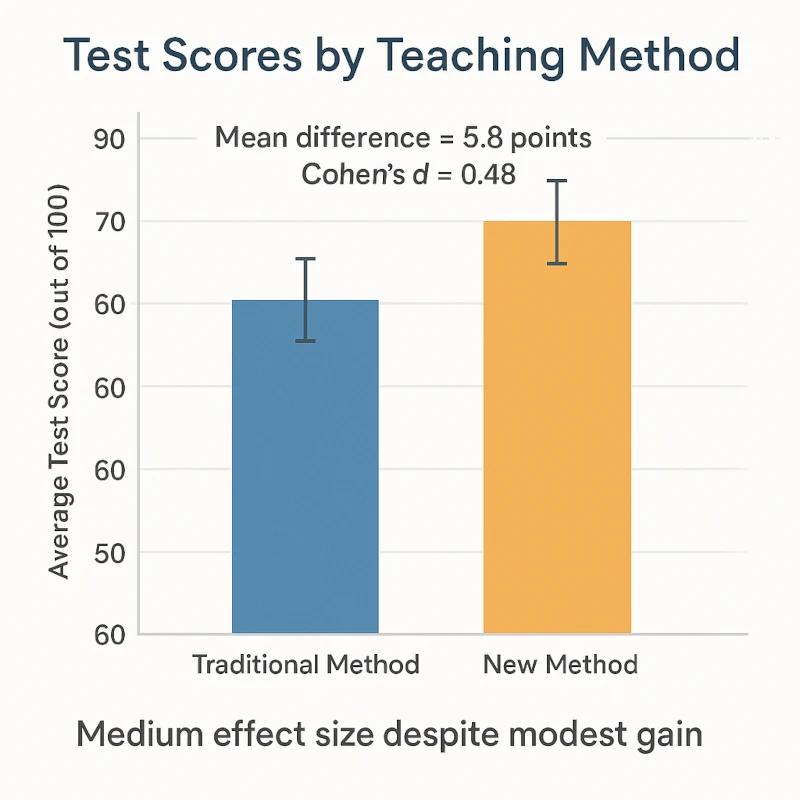
Example: Teaching Method Experiment

Group	Mean Score	SD	N
New Method	78.4	12.1	30
Traditional	72.6	11.8	30

Difference in means: $78.4 - 72.6 = 5.8$
Pooled SD ≈ $\sqrt{\frac{12.1^2 + 11.8^2}{2}} \approx 11.95$
Cohen’s d = $\frac{5.8}{11.95} \approx 0.48$

Interpretation: d ≈ 0.48 → medium effect size

Even without knowing the p-value, we now know the intervention had a moderately strong impact.

Two-group comparison with mean values and confidence intervals

Interpreting Cohen’s d: Rules of Thumb

Jacob Cohen proposed general guidelines for interpreting d:

Cohen’s d	Interpretation
0.2	Small effect
0.5	Medium effect
0.8	Large effect

These are benchmarks, not strict rules. Context matters: in education, a d of 0.4 might be very meaningful, in medicine, even d = 0.3 could justify a new treatment if scalable.

Use them as starting points — not final judgments.

A horizontal scale from 0 to 1+ with labeled zones (small/medium/large) and real-world analogies

When Should You Report Effect Size?

Best practices recommend reporting effect size in all empirical studies, especially when:

Comparing groups (t-tests, ANOVA)
Measuring associations (correlations, regression)
Conducting meta-analyses
Evaluating interventions (education, psychology, health)

Major journals (APA, APA-style publications) require effect sizes alongside p-values.

Other Common Effect Size Measures

While Cohen’s d is great for mean differences, other contexts require different metrics:

Test	Effect Size	Range
t-test (independent)	Cohen’s d, Hedges’ g	−∞ to +∞
ANOVA	Eta-squared (η²), Omega-squared (ω²)	0 to 1
Correlation	Pearson’s r	−1 to +1
Chi-square	Cramer’s V	0 to 1
Regression	R², f²	0 to 1

Why Effect Size Matters Researchers

Understanding effect size helps you:

Avoid overinterpreting statistically significant but trivial results
Compare findings across different studies and scales
Design better experiments (via power analysis)
Communicate results more honestly and transparently

Power analysis — used to determine required sample size — depends directly on expected effect size.

No effect size? You can’t plan a well-powered study.

Cosmic-scale artwork showing a balance between 'p-value' on one side and 'Effect Size' on the other, symbolizing the need to prioritize meaningful results in science.

Conclusion: Significance ≠ Importance

Let’s summarize the key takeaways:

p-value answers: “Is the effect real?”
Effect size answers: “How big is it?”
A result can be significant but trivial — always check both.
Cohen’s d is a powerful tool
Interpret using benchmarks: 0.2 (small), 0.5 (medium), 0.8 (large) — but consider context.

Statistical significance tells you if you should pay attention. Effect size tells you how much.